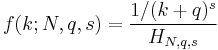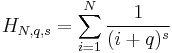Zipf–Mandelbrot law
| Parameters |  (integer) (integer) (real) (real)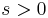 (real) (real) |
|---|---|
| Support | 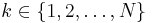 |
| PMF | 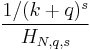 |
| CDF | 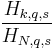 |
| Mean | 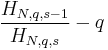 |
| Mode |  |
In probability theory and statistics, the Zipf–Mandelbrot law is a discrete probability distribution. Also known as the Pareto-Zipf law, it is a power-law distribution on ranked data, named after the linguist George Kingsley Zipf who suggested a simpler distribution called Zipf's law, and the mathematician Benoît Mandelbrot, who subsequently generalized it.
The probability mass function is given by:
where 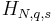 is given by:
is given by:
which may be thought of as a generalization of a harmonic number. In the formula, k is the rank of the data, and q and s are parameters of the distribution. In the limit as  approaches infinity, this becomes the Hurwitz zeta function
approaches infinity, this becomes the Hurwitz zeta function 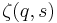 . For finite
. For finite  and
and 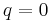 the Zipf–Mandelbrot law becomes Zipf's law. For infinite
the Zipf–Mandelbrot law becomes Zipf's law. For infinite  and
and 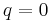 it becomes a Zeta distribution.
it becomes a Zeta distribution.
Contents |
Applications
The distribution of words ranked by their frequency in a random text corpus is generally a power-law distribution, known as Zipf's law.
If one plots the frequency rank of words contained in a large corpus of text data versus the number of occurrences or actual frequencies, one obtains a power-law distribution, with exponent close to one (but see Gelbukh & Sidorov, 2001).
In ecological field studies, the relative abundance distribution (i.e. the graph of the number of species observed as a function of their abundance) is often found to conform to a Zipf–Mandelbrot law.[1]
Within music, many metrics of measuring "pleasing" music conform to Zipf–Mandlebrot distributions.[2]
Notes
- ^ Mouillot, D; Lepretre, A (2000). "Introduction of relative abundance distribution (RAD) indices, estimated from the rank-frequency diagrams (RFD), to assess changes in community diversity". Environmental Monitoring and Assessment (Springer) 63 (2): 279–295. doi:10.1023/A:1006297211561. http://cat.inist.fr/?aModele=afficheN&cpsidt=1411186. Retrieved 24 Dec 2008.
- ^ Manris, B; Vaughan, D, Wagner, CS, Romero, J, Davis, RB. "Evolutionary Music and the Zipf-Mandelbrot Law: Developing Fitness Functions for Pleasant Music". Proceedings of 1st European Workshop on Evolutionary Music and Art (EvoMUSART2003) 611. http://shaunwagner.com/writings_computer_evomus.html.
References
- Mandelbrot, Benoît (1965). "Information Theory and Psycholinguistics". In B.B. Wolman and E. Nagel. Scientific psychology. Basic Books. Reprinted as
- Mandelbrot, Benoît (1968) [1965]. "Information Theory and Psycholinguistics". In R.C. Oldfield and J.C. Marchall. Language. Penguin Books.
- Zipf, George Kingsley (1932). Selected Studies of the Principle of Relative Frequency in Language. Cambridge, MA: Harvard University Press.
External links
- Z. K. Silagadze: Citations and the Zipf-Mandelbrot's law
- NIST: Zipf's law
- W. Li's References on Zipf's law
- Gelbukh & Sidorov, 2001: Zipf and Heaps Laws’ Coefficients Depend on Language